Scroll:Measurement >> Area of Triangle >> ps (1515)

Written Instructions:

For each Multiple Choice Question (MCQ), four options are given. One of them is the correct answer. Make your choice (1,2,3 or 4). Write your answers in the brackets provided..

For each Short Answer Question(SAQ) and Long Answer Question(LAQ), write your answers in the blanks provided.

Leave your answers in the simplest form or correct to two decimal places.


 

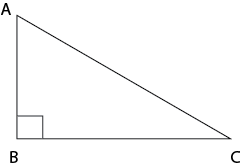
1)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 36cm.
What is the area of the triangle 




cm2


Answer:_______________




2)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 204cm.
What is the area of the triangle 




cm2


Answer:_______________




3)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 60cm.
What is the area of the triangle 




cm2


Answer:_______________




4)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 192cm.
What is the area of the triangle 




cm2


Answer:_______________




5)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 96cm.
What is the area of the triangle 




cm2


Answer:_______________




6)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 240cm.
What is the area of the triangle 




cm2


Answer:_______________




7)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 228cm.
What is the area of the triangle 




cm2


Answer:_______________




8)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 72cm.
What is the area of the triangle 




cm2


Answer:_______________




9)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 264cm.
What is the area of the triangle 




cm2


Answer:_______________




10)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 276cm.
What is the area of the triangle 




cm2


Answer:_______________




 

1)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 36cm.
What is the area of the triangle 




Answer: 54 cm2


SOLUTION 1 :

AB : BC : CA
3 : 4 : 5

 

Step 1:  3 + 4 +5 = 12 units

            12 units = 36 cm

             1 unit = 36 cm ÷ 12

                      = 3 cm

Step 2: AB → 3 units = 3 x 3 cm

                                   = 9 cm

Step 3:  BC → 4 units = 4 x 3 cm

                                   = 12 cm

Step 4: Area of triangle → 12 x 9 cm x 12 cm = 54 cm2



2)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 204cm.
What is the area of the triangle 




Answer: 1734 cm2


SOLUTION 1 :

AB : BC : CA
3 : 4 : 5

 

Step 1:  3 + 4 +5 = 12 units

            12 units = 204 cm

             1 unit = 204 cm ÷ 12

                      = 17 cm

Step 2: AB → 3 units = 3 x 17 cm

                                   = 51 cm

Step 3:  BC → 4 units = 4 x 17 cm

                                   = 68 cm

Step 4: Area of triangle → 12 x 51 cm x 68 cm = 1734 cm2



3)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 60cm.
What is the area of the triangle 




Answer: 150 cm2


SOLUTION 1 :

AB : BC : CA
3 : 4 : 5

 

Step 1:  3 + 4 +5 = 12 units

            12 units = 60 cm

             1 unit = 60 cm ÷ 12

                      = 5 cm

Step 2: AB → 3 units = 3 x 5 cm

                                   = 15 cm

Step 3:  BC → 4 units = 4 x 5 cm

                                   = 20 cm

Step 4: Area of triangle → 12 x 15 cm x 20 cm = 150 cm2



4)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 192cm.
What is the area of the triangle 




Answer: 1536 cm2


SOLUTION 1 :

AB : BC : CA
3 : 4 : 5

 

Step 1:  3 + 4 +5 = 12 units

            12 units = 192 cm

             1 unit = 192 cm ÷ 12

                      = 16 cm

Step 2: AB → 3 units = 3 x 16 cm

                                   = 48 cm

Step 3:  BC → 4 units = 4 x 16 cm

                                   = 64 cm

Step 4: Area of triangle → 12 x 48 cm x 64 cm = 1536 cm2



5)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 96cm.
What is the area of the triangle 




Answer: 384 cm2


SOLUTION 1 :

AB : BC : CA
3 : 4 : 5

 

Step 1:  3 + 4 +5 = 12 units

            12 units = 96 cm

             1 unit = 96 cm ÷ 12

                      = 8 cm

Step 2: AB → 3 units = 3 x 8 cm

                                   = 24 cm

Step 3:  BC → 4 units = 4 x 8 cm

                                   = 32 cm

Step 4: Area of triangle → 12 x 24 cm x 32 cm = 384 cm2



6)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 240cm.
What is the area of the triangle 




Answer: 2400 cm2


SOLUTION 1 :

AB : BC : CA
3 : 4 : 5

 

Step 1:  3 + 4 +5 = 12 units

            12 units = 240 cm

             1 unit = 240 cm ÷ 12

                      = 20 cm

Step 2: AB → 3 units = 3 x 20 cm

                                   = 60 cm

Step 3:  BC → 4 units = 4 x 20 cm

                                   = 80 cm

Step 4: Area of triangle → 12 x 60 cm x 80 cm = 2400 cm2



7)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 228cm.
What is the area of the triangle 




Answer: 2166 cm2


SOLUTION 1 :

AB : BC : CA
3 : 4 : 5

 

Step 1:  3 + 4 +5 = 12 units

            12 units = 228 cm

             1 unit = 228 cm ÷ 12

                      = 19 cm

Step 2: AB → 3 units = 3 x 19 cm

                                   = 57 cm

Step 3:  BC → 4 units = 4 x 19 cm

                                   = 76 cm

Step 4: Area of triangle → 12 x 57 cm x 76 cm = 2166 cm2



8)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 72cm.
What is the area of the triangle 




Answer: 216 cm2


SOLUTION 1 :

AB : BC : CA
3 : 4 : 5

 

Step 1:  3 + 4 +5 = 12 units

            12 units = 72 cm

             1 unit = 72 cm ÷ 12

                      = 6 cm

Step 2: AB → 3 units = 3 x 6 cm

                                   = 18 cm

Step 3:  BC → 4 units = 4 x 6 cm

                                   = 24 cm

Step 4: Area of triangle → 12 x 18 cm x 24 cm = 216 cm2



9)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 264cm.
What is the area of the triangle 




Answer: 2904 cm2


SOLUTION 1 :

AB : BC : CA
3 : 4 : 5

 

Step 1:  3 + 4 +5 = 12 units

            12 units = 264 cm

             1 unit = 264 cm ÷ 12

                      = 22 cm

Step 2: AB → 3 units = 3 x 22 cm

                                   = 66 cm

Step 3:  BC → 4 units = 4 x 22 cm

                                   = 88 cm

Step 4: Area of triangle → 12 x 66 cm x 88 cm = 2904 cm2



10)  

In the right-angled triangle shown below, the ratio of the length of sides AB : BC : CA is 3 : 4 : 5.
The perimeter of the triangle is 276cm.
What is the area of the triangle 




Answer: 3174 cm2


SOLUTION 1 :

AB : BC : CA
3 : 4 : 5

 

Step 1:  3 + 4 +5 = 12 units

            12 units = 276 cm

             1 unit = 276 cm ÷ 12

                      = 23 cm

Step 2: AB → 3 units = 3 x 23 cm

                                   = 69 cm

Step 3:  BC → 4 units = 4 x 23 cm

                                   = 92 cm

Step 4: Area of triangle → 12 x 69 cm x 92 cm = 3174 cm2